Hej! Det är mycket viktigt att ha koll på konjugatregeln och kvadreringsreglerna, då de ofta dyker upp i matematiken. Om du inte skulle ha riktigt det är den här sidan perfekt för dig!
Konjugatregeln
a^2-b^2=(a+b)(a-b)
Vi tittar på bilden nedanför, och sedan finns förklaringen under bilden.
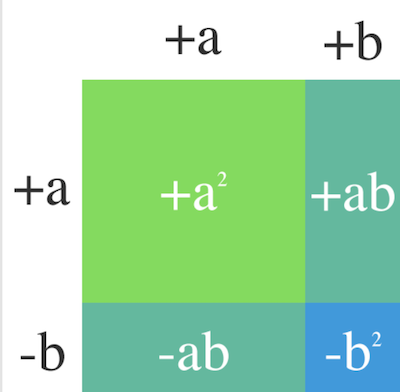
(a+b)(a-b)
uttrycks som sidorna i en fyrhörning, just denna är en kvadrat, men skulle lika gärna kunna vara en rektangel då både a och b är variabler. Arean får man som bekant genom att multiplicera basen med höjden.
a^2+ab-ab-b^2
Här har vi adderat ihop alla små rektanglar.
a^2+ab-ab-b^2=a^2-b^2=(a+b)(a-b)
Första kvadreringsregeln
(a+b)^2=a^2+2ab+b^2
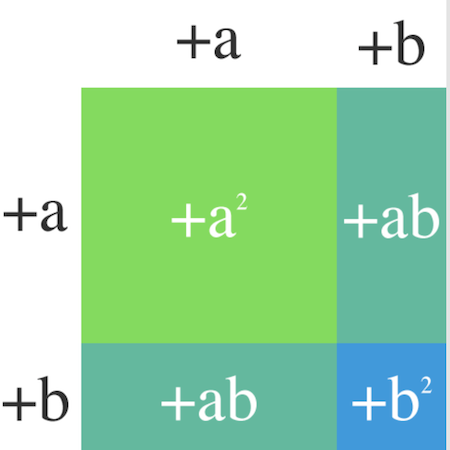
Räknas alla ”småafyrhörningar” i figuren och därmed hela arean får vi
a^2+ab+ab+b^2
Vi kan också få hela arean genom att beräkna
(a+b)(a+b)
Andra kvadreringsregeln
Denna regel säger att
(a-b)^2=a^2-2ab+b^2
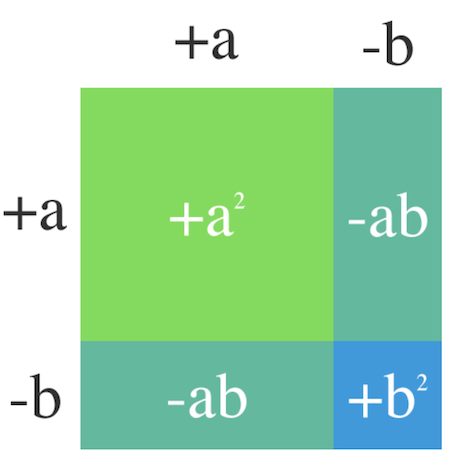
I princip samma som förra, vi har uttryckt
(a-b)^2 \text{ som } (a-b)(a-b)Här har vi adderat alla ”små” rektanglar inuti den stora.
a^2-ab-ab+b^2
Vi skriver
-ab-ab=-2ab
Dvs
(a-b)^2=a^2-2ab+b^2