Hej. Idag ska vi ha en genomgång av Pythagoras sats. Pythagoras sats introduceras i början av högstadiet, och därefter kommer den att följa med dig hela din utbildning, och sannolikt även hela din karriär om du fortsätter som ingenjör. Det har inte funnits ett enda nationellt prov i årskurs 9 som inte tagit upp Pythagoras sats, så även om du inte tycker matematik är jättekul är satsen nödvändig att kunna.
Pythagoras sats i korthet
För en rätvinklig triangel, dvs, en sådan där en vinkel är 90 grader gäller följande.
a^2+b^2=c^2

a och b kallas kateter, och c kallas hypotenusan. Dessa namn är viktiga att ha på minnet då de ofta dyker upp i läsuppgifter.
Bevis av Pythagoras sats
Det finns flera sätt att bevisa Pythagoras sats, förmodligen flera hundra, men vi har valt ett av de enklaste sätten. Detta bevis förkommer ofta i läroböckerna.
Vi börjar med en rätvinklig triangel i enlighet med figur 1 här ovanför. Vi har kateterna a och b, samt hypotenusan c.
Det vi gör nu är följande, vi tar triangeln, roterar den och ställer den på högkant. Detta gör vi tills vi får resultatet i figur 2. Nu har vi fyra trianglar och en kvadrat.
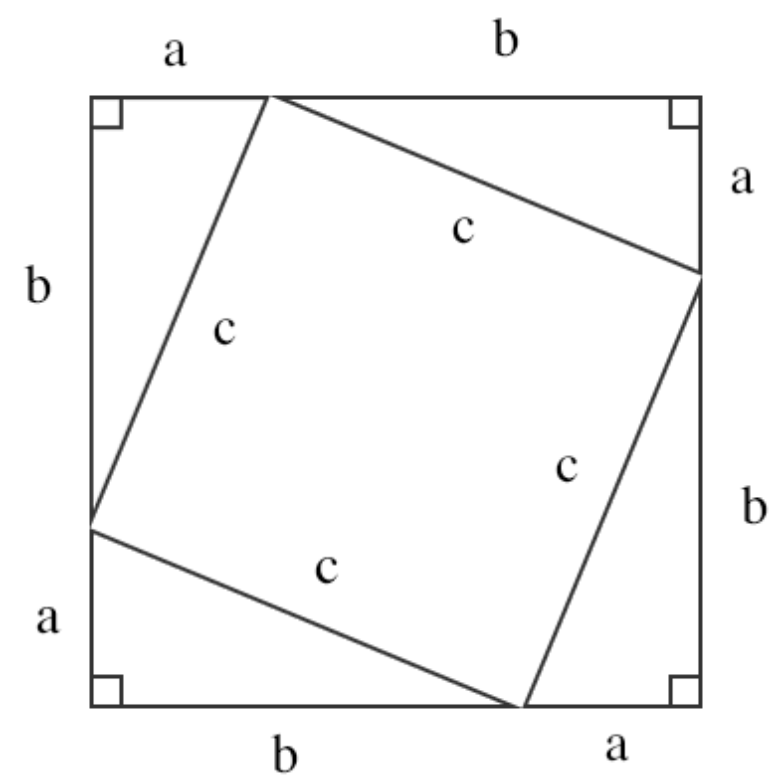
Nu kommer vi att uttrycka arean på två sätt.
Arean med hjälp av kvadratens sidor
Det första vi kommer göra nu är att beskriva arean för kvadraten med hjälp av kvadratens långa sidor. Sidorna i kvadraterna är b+a, och arean skrivs som basen multiplicerat med höjden.
A_1=(b+a)(b+a)=b^2+ba+ba+a^2
För att förtydliga, vi tänker bort alla sträck inuti och bryr oss inte om c i denna area. Det är bara hela arean av kvadraten vi är ute efter.
Ovanstående kan vi skrivas om som följande, vilket känns igen från kvadreringsregeln.
A_1=(b+a)(b+a)=a^2+2ab+b^2
Arean med hjälp av trianglar och vinklad kvadrat
Vi kan också skriva arean som summan av de fyra trianglarna, samt den vinklade kvadraten.
Arean av en triangel är basen multiplicerad med höjden dividerat med 2. Vi har fyra stycken trianglar. Arean av trianglarna kan då summeras som
\frac{ba}{2}+\frac{ba}{2}+\frac{ba}{2}+\frac{ba}{2}=4\frac{ba}{2}=2ba=2abTotala arean skrivs då som arean av trianglarna, adderat med arean av kvadraten. Kvadratens area är c^2 och totala arean är
A_1=2ab+c^2
Båda areorna är lika med varandra
Båda areorna är självklart lika stora, varvid
A_1=A_2
Vi tar in våra uttryck för areorna
a^2+2ab+b^2=2ab+c^2
.
Om vi subtraherar 2ab ur båda leden är vi framme.
a^2+b^2=c^2
Och så har vi bevisat Pythagoras sats!