Hej! Idag ska vi titta på ett problem som ofta dyker upp på prov.
Farmors jordgubbsland blir en ekvation
Jag ska göra ett rektangulärt jordgubbsland med arean 65 kvadratmeter. Den ena sidan ska vara (x-2) och den andra sidan ska vara (x+6). Hur långa blir sidorna i mitt jordgubbsland?
Ekvationsuppställning
Det är alltid bra att rita en bild av problemet.
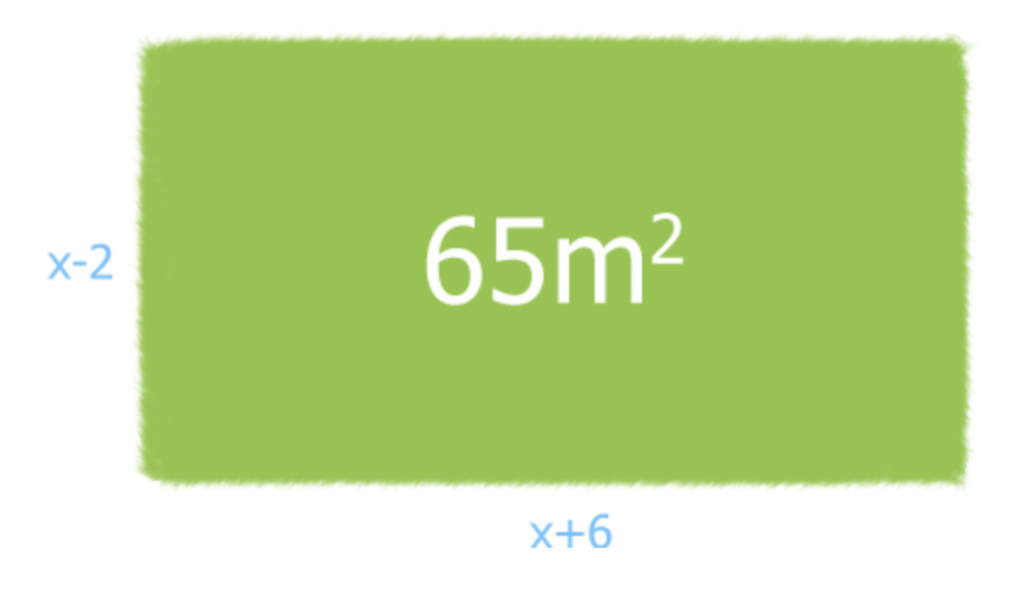
Vi tecknar ett uttryck för arean
A=(x+6)(x-2)
Eftersom det är givet att arean är 65 \, m^2 sätter vi nu dessa lika med varandra.
(x+6)(x-2)=65
Vi expanderar och förenklar uttrycket till
x^2-2x+6x-12=65 \\ x^2+4x-12=65 \\ x^2+4x-77=0
Vi använder pq-formeln.
x^2+4x-77=0 \\
x=-2 \pm \sqrt{4+77} \\
x=-2 \pm \sqrt{81} \\
x=-2 \pm 9 \\ \\
x_1 = 7 \\
x_2 = -11Den negativa lösningen måste vi förkasta, då sträckor inte kan vara negativa,
Farmors jordgubbsland är således 7-2=5 \, m och 7+6=13\,m.
Vi kontrollerar genom att multiplicera ihop basen med höjden, 5*13=65\,m^2.